Teaching PID controller in simple language (PID controller)
Temperature controllers have the task of comparing the actual temperature value of the process with the desired value (set point) and the command to the heater to adjust the temperature.
In traditional controllers, mechanical or electronic thermostats control the temperature only by connecting and disconnecting within the set range. Now we want to know more precisely what is PID controller.
With the emergence of microcontrollers and their diverse use in industries, new methods have been designed to control temperature. The PID controller is one of the most important and up-to-date methods.
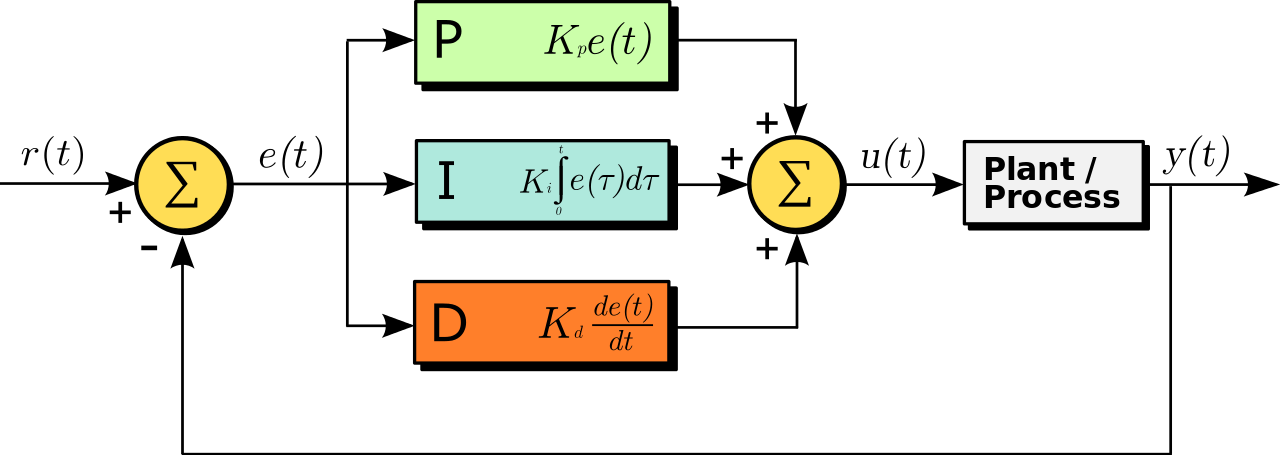
The PID controller (Proportional-Integral-Derivative controller) controls the temperature using three proportional, integral, and derivative variables, which helps improve the chamber’s thermal stability and uniform heating.
In this method, parameters such as overshoot and temperature variation are greatly reduced, and temperature regulation accuracy is significantly improved.
In laboratory ovens and furnaces used in industrial thermal processes, it is necessary to achieve consistent results, regardless of how the mass and moisture content of the heated material may change. In such cases, it is ideal to use PID control equipment.
In addition to thermal processes, PID controllers are widely used and useful in fluid flow control systems, motion system control, and other cases.
Heating processes are an example of the need for a PID controller. To ensure the stable quality of the product, the temperature inside the chamber must be kept within a narrow range. When a product is added or removed or when a thermal gradient is applied, a disturbance in the work process must be carefully considered and controlled.
Although the concept of PID seems simple, the basis of complex PID control calculations and achieving optimal performance requires the determination of specific process values for a wide range of influencing parameters.
The process of finding these values is called tuning. When the PID temperature controller is optimally tuned, the deviation from the set point is minimized. It will respond quickly to disturbance factors or changes compared to the set point, with minimal overshoot.
This article introduces how to tune a PID controller. Although many controllers can auto-tune, understanding how to tune will help you get the right performance.
PID control works based on feedback. The output of a device or a process, such as an oven, is measured and compared with a target or set point. If a discrepancy is detected, the correction amount is calculated and applied. The output is re-measured, and any corrections required are re-calculated.
PID includes three components: proportional, integral, and derivative. Not all controllers use all three of these math functions. Some processes can only be controlled at an acceptable level with proportional and integral functions.
However, a good PID temperature controller without overshoot requires adding a derivative function. (Note that this is why, even though the processor controls the temperature in many controllers, some fluctuation or temperature projection is still seen, and they do not provide complete thermal stability.)
In proportional control, the correction factor is determined by the amount of difference between the set point and the measured value. The problem is that this difference approaches zero, and by applying correction according to the result, the error never becomes zero.
The integral function works so that, considering the amount of error, the greater the difference between the set point and the measured value, the larger the correction factor is calculated.
However, when there is a delay in the correct response, an overshoot will occur and possibly lead to oscillation relative to the set point. Avoiding this is the purpose of the derivative function.

Each process has unique characteristics. Adjusting PID controller by Ziegler-Nichols method The airflow around the oven will be different, the ambient temperature may change, the air density and air pressure may change hour by hour or even the type of loading and the number of times the device door needs to be opened during operation. Therefore, PID settings must be chosen to accommodate these environmental changes and variations in use.
There are generally three approaches to determining an optimal combination of these settings:
- Tuning heuristics
- Autotune
- Manual Tuning
Often the processes are very complex, but with some information, particularly about the speed with which error correction is responded to, it is possible to achieve a rudimentary level of tuning.
Many rules have been developed over the years to answer how to tune a PID loop. The Ziegler-Nichols (ZN) law is the first and best known.
Ziegler and Nichols described two methods for tuning a PID controller loop, first published in 1942.
- The first method involves measuring the lag or response delay and then taking time to reach a new output value.
- The second method depends on the time to reach the steady-state oscillation. In both methods, the obtained values are entered in a table to calculate the values of gain, reset time, and rate.
The ZN method has problems. In some programs, it creates an aggressive response in terms of overshoot and swing. Another problem is that it can be time-consuming in processes that react slowly.
For these reasons, some people who work on the control system prefer other rules such as Tyreus-Luyben or Rivera, Morari, and Skogestad.
Many controllers are sold today that are automatically tuned. Performance details vary between manufacturers, but all follow the rules explained earlier.
The controller ‘learns’ how the process responds to a disturbance or change in the set point and calculates the appropriate controller PID settings.
In the case of a heat controller, when Auto-Tune is selected, the controller activates an output. By observing the Delay and Rate at which the change occurs, Appropriate P, I, and D settings are calculated, and even fine manual adjustment is possible if needed.
(This controller needs a set point at least 10 degrees Celsius higher than the current temperature to perform the automatic adjustment.)
Newer and more sophisticated controllers combine fuzzy logic with automatic tuning. This provides one way to deal with imprecision and non-linearity.
PID controller is used to manage many processes. The correction factors are calculated by comparing the output values to the set point and using a gain that minimizes overshoot and fluctuation. At the same time, these effective changes will be applied as soon as possible.
PID tuning involves creating the appropriate gain value to control the process. While this can be done manually or using heuristics, most modern controllers offer Auto-Tune.
However, for professional control, it is very important to understand what happens after the button is pressed.






